Adman梯度下降算法核心思想是，对于每个参数，根据其梯度的历史信息，动态调整其学习率从而实现更快的收敛和更好的性能。Adman梯度下降算法使用两个参数，一个是动量参数，另一个是自适应学习率参数。

动量参数用于加速参数的更新

自适应学习率参数则根据参数梯度的历史信息，动态调整参数的学习率。

在学习adam梯度下降算法之前，有必要先了解一下梯度下降算法和动量梯度下降算法。

梯度下降算法

梯度下降算法(Gradient Descent, GD)是深度学习的核心之一，用于最小化目标函数。其基本思想是，在每次迭代中，沿着目标函数的负梯度方向更新参数，从而逐步逼近最优解。
随机梯度下降算法(Stochastic Gradient Descent, SGD)是梯度下降算法的一种改进，它每次迭代只使用一部分样本进行计算，从而加快了训练速度。
动量梯度下降算法(Momentum Gradient Descent, MGD)是梯度下降算法的另一种改进，它引入了动量参数，用于加速参数的更新。
自适应学习AdaGrad算法、RMSProp算法训练过程中可以动态调整学习率，从而实现更快的收敛和更好的性能。
Adam梯度下降算法(Adaptive Moment Estimation, Adam)是梯度下降算法的另一种改进，它结合了动量梯度下降算法和自适应学习率算法，是一种常用的优化算法。

在此之前,复习下损失函数。

损失函数

在深度学习中，网络参数的迭代更新由损失函数的梯度决定。梯度下降算法通过计算损失函数相对于参数的梯度，然后沿着梯度的负方向更新参数，从而逐步逼近最优解。

假设一个很简单的线性回归模型，输入为x,输出为y，模型参数为w和b。

其模型为：

\hat{y} = wx + b

损失函数为：

L = \frac{1}{2}(\hat{y} - y)^2

梯度下降算法的更新规则为：

w = w - \eta \frac{\partial L}{\partial w}

b = b - \eta \frac{\partial L}{\partial b}

其中， $\eta$ 为学习率， $\frac{\partial L}{\partial w}$ 和 $\frac{\partial L}{\partial b}$ 分别为损失函数L对参数w和b的梯度。

\theta = \theta - \eta \nabla L(\theta)

其中， $\theta$ 为参数向量， $\nabla L(\theta)$ 为损失函数L对参数 $\theta$ 的梯度向量。
可以看出，每次更新参数时，都会乘以一个系数 $\eta$ ，如果 $\eta$ 过大，可能会导致参数更新过大，从而错过最优解；如果 $\eta$ 过小，可能会导致参数更新过慢，从而收敛速度过慢。因此，选择合适的学习率是非常重要的。

而且对于高维情况，普通梯度下降算法存在局限性
例如：

输入元素: $x$ 、 $y$
损失函数为: $f(x,y) = x^2 + y^2$
梯度求偏导: $\frac{\partial f}{\partial x}$ 、 $\frac{\partial f}{\partial y}$ :
$\frac{\partial f}{\partial x} = 2x$ $\frac{\partial f}{\partial y} = 2y$
更新参数： $x$ 、 $y$
$x = x - \eta \frac{\partial f}{\partial x} = x - 2\eta x$ $y = y - \eta \frac{\partial f}{\partial y} = y - 2\eta y$

示例代码：

import numpy as np
import matplotlib.pyplot as plt
from matplotlib import cm

# 配置中文字体（可选）
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False

# 定义损失函数（示例使用二次函数）
def loss_function(x, y):
    return x**2 + y**2

# 计算梯度
def compute_gradient(x, y):
    dx = 2*x
    dy = 2*y
    return dx, dy

# 梯度下降参数设置
lr = 0.1       # 学习率
steps = 15     # 迭代次数
start_point = (-4, 3.5)  # 初始点

# 生成网格数据
x = np.linspace(-5, 5, 100)
y = np.linspace(-5, 5, 100)
X, Y = np.meshgrid(x, y)
Z = loss_function(X, Y)

# 执行梯度下降
path = [start_point]
current_x, current_y = start_point
for _ in range(steps):
    grad_x, grad_y = compute_gradient(current_x, current_y)
    current_x -= lr * grad_x
    current_y -= lr * grad_y
    path.append((current_x, current_y))

# 转换为数组便于绘图
path = np.array(path)
x_path, y_path = path[:,0], path[:,1]
z_path = loss_function(x_path, y_path)

# 创建三维画布
fig = plt.figure(figsize=(12, 8))
ax = fig.add_subplot(111, projection='3d')

# 绘制损失函数曲面
surf = ax.plot_surface(X, Y, Z, cmap=cm.coolwarm,
                       alpha=0.6, linewidth=0,
                       antialiased=False)

# 绘制梯度下降路径
ax.plot(x_path, y_path, z_path, 'r-o', 
        markersize=8, linewidth=2,
        markerfacecolor='yellow')

# 添加梯度箭头
for i in range(len(path)-1):
    dx = path[i+1,0] - path[i,0]
    dy = path[i+1,1] - path[i,1]
    dz = z_path[i+1] - z_path[i]
    ax.quiver(path[i,0], path[i,1], z_path[i],
              dx*0.8, dy*0.8, dz*0.8,
              color='black', arrow_length_ratio=0.1)

# 添加标签和标题
ax.set_xlabel('X 参数', labelpad=12)
ax.set_ylabel('Y 参数', labelpad=12)
ax.set_zlabel('损失值', labelpad=12)
ax.set_title('三维梯度下降过程可视化', y=1.02, fontsize=14)

# 设置观察角度
ax.view_init(elev=30, azim=-140)

# 显示颜色标尺
fig.colorbar(surf, shrink=0.5, aspect=5)

# 显示图形
plt.tight_layout()
plt.show()

可视化结果：
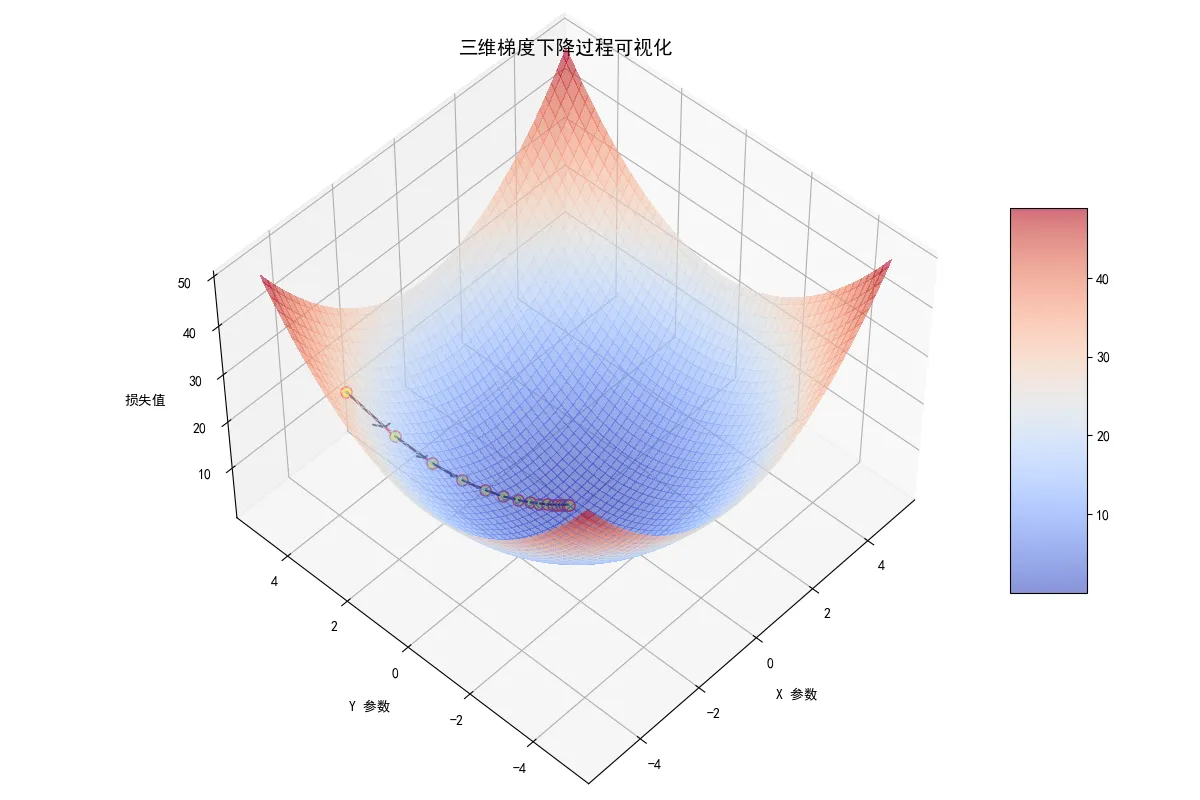
images/梯度更新.png

缺点：

梯度下降算法在训练过程中可能会陷入局部最小值，导致模型无法收敛到全局最优解。
梯度下降算法的学习率需要手动调整，如果学习率过大，可能会导致模型在最优解附近震荡，如果学习率过小，可能会导致模型收敛速度过慢。

动量梯度下降算法

不同于上面的梯度下降算法，动量梯度下降算法引入了历史梯度信息(可以理解为保留上次梯度更新方向的一定力)。

公式为：

v = \beta v - \eta \nabla L(\theta)

$v$ 为历史梯度信息的保留量， $\beta$ 为动量参数，取值范围为0到1之间，通常取0.9。 $\eta$ 为学习率， $\nabla L(\theta)$ 为损失函数L对参数 $\theta$ 的梯度向量。
参数更新变为：

\theta = \theta + v

$\theta$ 为参数向量。

优点：

动量梯度下降算法可以加速参数的更新，减少训练时间。
动量梯度下降算法可以避免局部最小值，提高模型的收敛速度。

缺点：

动量梯度下降算法需要手动调整动量参数和学习率，如果参数设置不当，可能会导致模型收敛速度过慢或者震荡。

学习率

学习率是梯度下降算法中最重要的参数之一，它决定了参数更新的步长。如果学习率过大，可能会导致模型在最优解附近震荡，如果学习率过小，可能会导致模型收敛速度过慢。因此，选择合适的学习率是非常重要的。

引入变量 $r$ (AdaGrad算法2011)

r = r + \nabla L(\theta)^2

重点：
- $r$是一个变量，其值随着迭代不断增大，导致学习率下降。
- $r$每次增加的量由计算的梯度值$\nabla L(\theta)$决定。
参数更新：

\theta = \theta - \frac{\eta}{\sqrt{r} + \epsilon} \nabla L(\theta)

$\epsilon$ 为防止除0操作，通常取一个很小的值，如 $10^{-8}$ 。

这样当梯度变化较大时，$r$增加的多，学习率减小的快，当梯度变化较小时，$r$增加的少，学习减小的慢。

问题：AdaGrad算法 $r$ 值只与梯度有关，可能导致学习率过早的变小。

引入变量 $\rho$ (RMSProp算法2012)

r = \rho v + (1 - \rho) \nabla L(\theta)^2

\theta = \theta - \frac{\eta}{\sqrt{r} + \epsilon} \nabla L(\theta)

其中： $\rho$ 为手动调节参数。

Adam梯度下降算法(2014)

Adam梯度下降算法结合了动量梯度下降算法和自适应学习率算法，是一种常用的优化算法。

自适应动量：

v = \rho_1 v + (1 - \rho_1) \nabla L(\theta)

$\rho_1$ 是动量参数。

r = \rho_2 r + (1 - \rho_2) \nabla L(\theta)^2

$\rho_2$ 是自适应学习率参数。

修正动量和学习率：

\widehat{v} = \frac{v}{1 - \rho_1^t}

\widehat{r} = \frac{r}{1 - \rho_2^t}

$t$ 为迭代次数，修正后使得在训练之初，动量和学习率比较大，帮助快速收敛。

参数更新：

\theta = \theta - \frac{\eta \widehat{v}}{\sqrt{\widehat{r}} + \epsilon} v

Adman梯度下降

梯度下降算法

损失函数

动量梯度下降算法

学习率

Adam梯度下降算法(2014)

onnx+opencv+opencl